Frequency bands 頻帶與頻譜配置
通訊使用的是電磁波頻譜(electromagnetic spectrum)中的特定範圍。但因為傳輸距離(低頻可傳更遠)、穿透能力(低頻能穿牆,高頻容易被阻擋)、頻寬需求(高頻可提供較大頻寬,適合高速傳輸)、天線大小、設備成本、干擾與法規限制等因素,並非所有頻率都適合用於所有通訊任務。
無線電頻譜分類(Radio Spectrum)
| 頻帶縮寫 | 全名 | 中文名稱 | 頻率範圍(約略) | 常見應用 |
|---|---|---|---|---|
| VLF | Very Low Frequency | 超低頻 | 3 – 30 kHz | 潛艇通訊、長波導航 |
| LF | Low Frequency | 低頻 | 30 – 300 kHz | 航海、AM 廣播(長波) |
| MF | Medium Frequency | 中頻 | 300 kHz – 3 MHz | AM 廣播 |
| HF | High Frequency | 高頻 | 3 – 30 MHz | 短波廣播、國際通訊 |
| VHF | Very High Frequency | 甚高頻 | 30 – 300 MHz | FM 廣播、電視、航空無線電 |
| UHF | Ultra High Frequency | 超高頻 | 300 MHz – 3 GHz | 行動通訊、Wi-Fi、電視 |
| SHF | Super High Frequency | 特高頻 | 3 – 30 GHz | 衛星、雷達、5G 毫米波 |
| EHF | Extra High Frequency | 極高頻 | 30 – 300 GHz | 天文觀測、6G、毫米波通訊 |
| UV | Ultraviolet Light | 紫外線 | >300 THz | 非通訊用途(醫療、化學反應) |
ISM bands
「ISM 頻段」是免授權(license-free)的頻率範圍,開放給工業、科學、醫療及消費性應用,雖然讓成本下降,但也讓干擾上升
| 頻率範圍 (MHz / GHz) | 區域 / 備註 | 典型應用 |
|---|---|---|
| 13.553 – 13.567 MHz | 全球通用 | RFID、近場通訊、感測裝置 |
| 26.957 – 27.283 MHz | 全球通用 | 工業控制、遙控玩具、低速資料傳輸 |
| 40.66 – 40.70 MHz | 全球通用 | 遙控器、簡易通訊設備 |
| 433 – 464 MHz | 歐洲常用 | 無線感測器、遙控門鎖、IoT 裝置 |
| 900 – 928 MHz | 美洲常用 | RFID、LoRa、ZigBee、IoT 傳輸 |
| 2.4 – 2.5 GHz | 全球通用 | Wi-Fi、藍牙(Bluetooth)、ZigBee、微波爐 |
| 5.725 – 5.875 GHz | 全球通用 | Wi-Fi(5 GHz 頻段)、無線影像傳輸 |
| 24 – 24.25 GHz | 全球通用 | 工業感測、毫米波雷達、短距離資料傳輸 |
Modulation 調變技術
這節將說明如何將數位訊號轉換成可在無線通道中傳輸的類比波形,例如 ASK、PSK、QAM 等。
利用無線電波傳送資料(Transmitting Data Using Radio Waves)
- 發送端(Sender):能發射無線電波。
- 接收端(Receiver):能偵測該電波的存在與其特性(參數)。
- 無線電波的數學模型為一個隨時間變化的正弦波:
$s(t) = A(t) \sin(2 \pi f(t) t + \phi(t))$
其中:
| 參數 | 意義 | 對應英文 |
|---|---|---|
| A(t) | 幅度(決定波的強度) | Amplitude |
| f(t) | 頻率(決定波的振動次數) | Frequency |
| $\phi(t)$ | 相位(決定波的起始角度) | Phase |
調變的基本想法(Modulation Concept)
- 傳輸資料的本質:改變載波波形的某個參數來代表資料。
- 接收端再依波形變化解出原始資料。
| 類型 | 方法 | 名稱 | 特性 |
|---|---|---|---|
| 類比調變(Analog Modulation) | 參數可取任意值 | Amplitude / Frequency / Phase Modulation | 波形連續變化,用於語音、影像等模擬信號 |
| 數位調變(Digital Keying) | 參數取有限離散值 | ASK / FSK / PSK(鍵控法) | 適合數位資料,抗干擾能力強 |
常見的數位調變方式(Digital Keying Examples)
| 名稱 | 中文名稱 | 原理說明 | 示意 |
|---|---|---|---|
| ASK (Amplitude Shift Keying) | 幅移鍵控 | 用資料(0/1)改變載波的振幅大小 | 波高改變 |
| FSK (Frequency Shift Keying) | 頻移鍵控 | 用資料改變載波的頻率高低 | 週期長短改變 |
| PSK (Phase Shift Keying) | 相移鍵控 | 用資料改變載波的相位角度 | 波形偏移位置不同 |
💡 例如:
在 PSK 中,0可能代表相位 0°,1代表 180°;
而在 FSK 中,0用低頻率,1用高頻率。
接收端的任務:解調(Demodulation)
接收端觀察接收到的波形,找出最接近哪一種已知的波形模式,
並推測出原本代表的資料位元(bit)。為了能準確還原:
- 必須建立「資料 ↔ 波形」的一對一對應關係。
- 類比信號因連續變化,難以完全重建;
數位信號較容易區分與還原。
解調的挑戰(Demodulation Problems)
| 問題類型 | 說明 |
|---|---|
| 載波同步(Carrier Synchronization) | 發送端與接收端的頻率可能因溫度、老化或時鐘漂移而不一致,造成波形錯位。 |
| 位元/符號同步(Bit or Symbol Synchronization) | 接收端需判斷每個符號的起點與終點,否則會錯讀資料。 |
| 框架同步(Frame Synchronization) | 必須知道封包(frame)從何開始與結束,才能正確組合資料。 |
| 通道失真(Channel Distortion) | 實際接收的波形通常被雜訊、多路徑等干擾所扭曲,導致「接收到的訊號 ≠ 傳送的訊號」。 |
訊號失真與無線通道(Signal Distortion – Wireless Channels)
無線傳輸會扭曲任何發射的訊號,因此接收端收到的訊號 ≠ 傳送端發出的訊號,且造成接收端無法確定原始的位元序列是什麼。這些失真效應統稱為:無線通道(Wireless Channel)。
主要失真來源(Sources of Distortion)
| 失真來源 | 中文名稱 | 說明 |
|---|---|---|
| Attenuation | 衰減 | 隨距離增加,能量分佈於更大範圍,訊號強度下降。 |
| Reflection / Refraction | 反射 / 折射 | 電波遇到表面反彈或穿入不同介質產生彎折。 |
| Diffraction | 繞射 | 電波經過尖銳邊緣時產生新的波前。 |
| Scattering | 散射 | 表面粗糙時產生多重反射,形成雜訊性干擾。 |
| Doppler Fading | 多普勒衰落 | 由於相對移動造成頻率偏移,使中心頻率產生漂移。 |
衰減與路徑損失(Attenuation & Path Loss)
- 衰減的效果可用「路徑損失(Path Loss)」表示。
- 接收功率 (P_r) 會隨著距離 (d) 增加而減少。
Friis 自由空間方程式(Free-space Equation)
$\frac{P_r}{P_t} = \frac{A_t A_r}{(\lambda d)^2} \times \text{(gain factors)}$
| 符號 | 意義 |
|---|---|
| (P_t) | 發射功率 |
| (P_r) | 接收功率 |
| (A_t, A_r) | 發射與接收天線的有效孔徑(aperture) |
| (\lambda) | 波長 |
| (d) | 傳輸距離 |
非視距傳播(Non-Line-of-Sight, NLOS)
無線電波不只走「直線」路徑,還會:
- 經由牆壁、地面、建築物反射或繞射。
- 各路徑長度不同 → 造成「延遲展開(Delay Spread)」。
- 結果:同一訊號在不同時間抵達接收端,產生干涉。
因此簡單的自由空間模型(1/d²)不足以描述真實環境中的多路徑效應。
廣義衰減模型(Generalized Path-Loss Model)
加入環境因素
- 牆壁、障礙物會造成更嚴重的衰減。
- 定義 路徑損失指數(Path-loss exponent, γ):
$P_r \propto \frac{1}{d^{\gamma}}, \quad \text{其中 } \gamma > 2$
| 環境類型 | 常見 γ 值 |
|---|---|
| 自由空間(Free space) | 2 |
| 室內(Indoor) | 3–5 |
| 城市環境(Urban) | 2.7–4 |
以線性形式表達
$P_{\text{recv}}(d) = P_{\text{recv}}(d_0) \cdot \left( \frac{d_0}{d} \right)^{\gamma}$
| 符號 | 意義 |
|---|---|
| $P_{\text{recv}}(d)$ | 接收功率(距離 (d)) |
| $P_{\text{recv}}(d_0)$ | 參考距離 (d_0) 下的接收功率 |
| $d$ | 傳輸距離 |
| $\gamma$ | 路徑損失指數(path-loss exponent),描述訊號強度衰減的速度 |
距離越遠,功率會依距離的 $(-\gamma)$ 次方遞減。
例如:在自由空間中 $(\gamma = 2)$,即功率 ∝ $(1/d^2)$。
若改以對數形式(Logarithmic Form, in dB)
$PL(d)[\text{dB}] = PL(d_0)[\text{dB}] + 10\gamma \log_{10}\left(\frac{d}{d_0}\right)$
| 符號 | 意義 |
|---|---|
| $PL(d)$ | 距離 (d) 的路徑損失(Path Loss) |
| $PL(d_0)$ | 參考距離 (d_0) 的路徑損失 |
| $10\gamma \log_{10}\left(\frac{d}{d_0}\right)$ | 額外衰減量(隨距離增加) |
工程上常使用 dB 表示功率比例,因此這個式子是將功率衰減的乘法關係轉為加法關係,方便運算與繪圖。
統計性通道建模(Shadowing Effect)
為了模擬環境中隨機遮蔽效應(shadowing),通常在對數(dB)形式的損失模型中加入隨機變數:
$PL(d)[\text{dB}] = PL(d_0)[\text{dB}] + 10\gamma \log_{10}!\left(\frac{d}{d_0}\right) + X_{\sigma}[\text{dB}]$
| 符號 | 名稱 | 說明 |
|---|---|---|
| (PL(d)) | 距離 (d) 的路徑損失(Path Loss) | 單位為 dB |
| (PL(d_0)) | 參考距離 (d_0) 的路徑損失 | 通常取 1 m 或 100 m |
| (\gamma) | 路徑損失指數(Path-loss exponent) | 決定訊號隨距離衰減的快慢(自由空間約為 2,城市環境可達 3–5) |
| (10\gamma \log_{10}(d/d_0)) | 決定距離對功率的平均衰減 | 越遠衰減越多 |
| (X_{\sigma}) | 陰影衰落項(Shadowing term) | 服從平均值 0、變異數 (\sigma^2) 的高斯分布 (N(0, \sigma^2)),用以模擬障礙物導致的隨機功率波動 |
從波到位元(From waves to bits)
無線通訊中的干擾來源(Noise and Interference)
前面只考慮單一傳送端與其多路徑效應(同一訊號在不同路徑反射回來),但實際環境中還有兩種額外的干擾來源。
| 類型 | 中文名稱 | 說明 |
|---|---|---|
| Noise(雜訊) | 電子元件雜訊 | 來自接收端硬體內部,如放大器、接收器電路。與溫度相關。通常建模為: 加性高斯白雜訊 (AWGN) — 平均值 0,時間上不相關。 |
| Interference(干擾) | 無線通訊之間的相互影響 | - 同頻干擾 (Co-channel interference):其他使用相同頻道的傳送端。 - 鄰頻干擾 (Adjacent-channel interference):其他使用鄰近頻段的訊號,由於濾波器不完美而滲入。 |
從波形還原資料:符號與位元錯誤(Symbols and Bit Errors)
- 接收端需要從扭曲或受干擾的波形中,判斷出原本的符號(symbol)。
- 若判斷錯誤,就會發生符號錯誤(symbol error)或位元錯誤(bit error)。
SINR(Signal-to-Interference-and-Noise Ratio)
衡量「有用訊號」相對於「雜訊與干擾」的強度比值。
$\text{SINR} = 10 \log_{10} \left( \frac{P_{\text{recv}}}{N_0 + \sum_{i=1}^{k} I_i} \right)$
| 符號 | 名稱 | 說明 |
|---|---|---|
| $P_{\text{recv}}$ | 接收訊號功率 (Received Signal Power) | 想要接收的目標訊號強度 |
| $N_0$ | 雜訊功率 (Noise Power) | 通常由接收機熱雜訊產生,與溫度、頻寬相關 |
| $\sum_{i=1}^{k} I_i$ | 干擾功率總和 (Total Interference Power) | 來自其他 (k) 個使用相同或鄰近頻道的干擾源 |
| $\log_{10}$ | 對數轉換 | 將功率比轉換成 dB(分貝)單位 |
若只考慮雜訊(無干擾),則為常見的 SNR(Signal-to-Noise Ratio)。
$\text{SINR} = \frac{S}{I + N}$
| 符號 | 意義 |
|---|---|
| (S) | 有效訊號功率 |
| (I) | 干擾功率 |
| (N) | 雜訊功率 |
雜訊功率與頻寬的關係
$N = N_0 \times B$
| 符號 | 意義 |
|---|---|
| $N_0$ | 雜訊功率譜密度(Noise Spectral Density),表示每 1 Hz 頻寬的雜訊功率 |
| $B$ | 系統頻寬(Hz) |
| $N$ | 總雜訊功率 |
SINR 與 BER(Bit Error Rate)的關係
- **BER(位元錯誤率)**表示接收到的位元中有多少被誤判。
- BER 的大小取決於:
- 調變方式(Modulation Scheme)
- SINR 值(訊號品質)
- 每個位元的能量 (E_b)
SINR 可用來計算在特定調變方式下的 位元錯誤率(BER)。
$\text{BER(SINR)} = 0.5 e^{-\frac{E_b}{N_0}}$
這是一個近似公式(特別常見於 BPSK 調變),表示:
- 當 (E_b/N_0) 增加(即訊號品質變好),BER 會以指數方式下降。
能量比關係式
$\frac{E_b}{N_0} = \text{SINR} \times \frac{1}{R}$
| 符號 | 名稱 | 說明 |
|---|---|---|
| (E_b) | 每個位元的能量(Energy per bit) | 用於解調與錯誤修正 |
| (N_0) | 雜訊功率譜密度(Noise Spectral Density) | 每 1 Hz 頻寬內的平均雜訊功率 |
| (R) | 位元率(Bit rate) | 單位:bit/s |
若位元率 (R) 提高(資料傳得更快),則每個位元能分到的能量變少 → (E_b/N_0) 降低 → BER 變高。
SNR 與 (E_b/N_0) 的對應關係
$\text{SNR} = \frac{E_s}{N_0} = \frac{E_b \times R}{N_0}$
| 符號 | 意義 |
|---|---|
| (E_s) | 每個符號的能量(Energy per symbol) |
| (E_b) | 每個位元的能量 |
| (R) | 位元率(bit/s) |
| (N_0) | 雜訊功率譜密度 |
| 名稱 | 定義 | 物理意義 |
|---|---|---|
| SINR | $\frac{P_{\text{signal}}}{P_{\text{noise}} + P_{\text{interference}}}$ | 真實環境中的訊號品質 |
| SNR | $\frac{P_{\text{signal}}}{P_{\text{noise}}}$ | 理想情況下的訊號雜訊比 |
| (E_b/N_0) | 單位位元能量與雜訊功率密度比 | 衡量通訊鏈路的效率 |
| BER | 錯誤位元比例 | 衡量實際傳輸可靠度 |
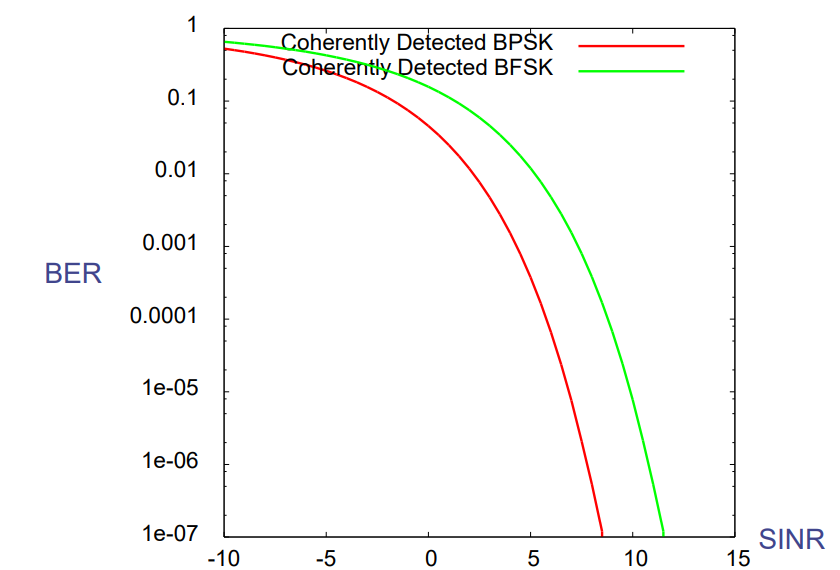
隨著 SINR 增加(訊號變清晰),BER 以指數方式下降
通道模型(Channel models)
analog signal model
| 模型名稱 | 假設條件 | 數學表達式 / 分布 | 通道特性 | 適用環境 |
|---|---|---|---|---|
| AWGN(Additive White Gaussian Noise)模型 | - 傳輸功率與衰減固定不變 - 雜訊為時間上不相關的高斯白雜訊 - 有 line-of-sight(直接通訊) |
( r(t) = s(t) + n(t) ) 其中: (r(t)):接收訊號 (s(t)):傳送訊號 (n(t)):白高斯雜訊 |
- SNR 為常數 - 僅考慮雜訊,不考慮多路徑 - 理想化模型(基準情境) |
自由空間、理論模擬、基準測試 |
| Rayleigh Fading(瑞利衰落)模型 | - 無直視路徑(NLoS) - 訊號由多條反射路徑隨機疊加 |
振幅服從 Rayleigh 分布 | - 多路徑效應明顯 - 訊號強度快速變化(深度衰落頻繁) |
都市高樓區、室內環境 |
| Rice Fading(萊斯衰落)模型 | - 有一條主導直視路徑(LoS)+ 多條反射路徑 | 振幅服從 Rice 分布 (K) 因子表示 LoS 與多路徑能量比 |
- 同樣包含多路徑,但有強主徑分量 - 較穩定,衰落程度較低 - 可以算是前兩者的混合 |
開放區域、有明顯 LoS 的場景(如基地台可視) |
digital model
只把模型分成兩種狀態,例如 Binary Symmetric Channel (BSC),只關心「位元是否正確接收」,可簡化成:
- 每個位元有固定錯誤機率 𝑝
- 各位元錯誤彼此獨立
| 狀態 | 概率 |
|---|---|
| 傳對(bit 保持不變) | (1 - p) |
| 傳錯(bit 翻轉) | (p) |
現實狀況如何應對?
上面提到了很多模型理論,但事實上現實世界是極端的,不可能存在理論上的 wireless channel。所以現實世界在硬體已經無法再提升的情況下,為了降低通道導致的錯誤率,軟體層面會採用:
| 技術 | 目的 | 功能 |
|---|---|---|
| FEC (Forward Error Correction) | 為了預防 | 在傳輸前加入冗餘位元,讓接收端可自動修正錯誤 |
| ARQ (Automatic Repeat Request) | 事後補救 | 發現錯誤時要求重新傳輸(常與 FEC 結合成 Hybrid ARQ) |
收發機設計(Transceiver Design)
在前面的章節介紹了調變的方式、模型通道,這邊要來做最後的總結,也就是收發機設計的核心目標。
調變方式選擇與取捨
我們需要根據當下條件,適時選擇合適的調變技術,這些調件包含:
- 所需資料率(Data Rate)
- 可達符號率(Symbol Rate)
- 實作複雜度(Implementation Complexity)
- 允許錯誤率(BER 要求)
- 通道特性(Channel Conditions)
而調變需要注意符號率與資料率的取捨(Trade-offs),因為調變方式會影響功率消耗。當傳得越快(高 symbol rate)可更快進入休眠以省電,但高資料率也可能導致錯誤率上升與功耗增加。
- Symbol Rate 符號率:決定每秒發送的符號數;每個符號可攜帶多個位元。例如同樣符號率下,QPSK 資料率是 BPSK 的兩倍:
- BPSK → 1 符號 = 1 位元,可以代表 2 個情況
- QPSK → 1 符號 = 2 位元,可以代表 4 個情況
- 8PSK → 1 符號 = 3 位元,可以代表 8 個情況
- 16APSK → 1 符號 = 4 位元,可以代表 16 個情況
- 32APSK → 1 符號 = 5 位元,可以代表 32 個情況
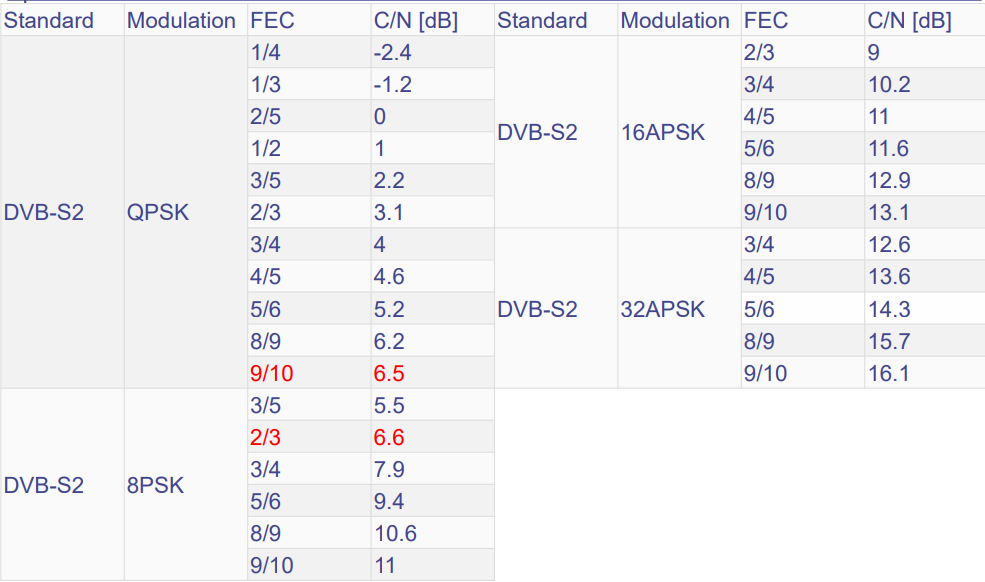
說明
FEC 1/4 代表 4 個 bit 只有一個傳 data,其他容錯用,所以當 channel 不好的時候就可以選這個。C/N [dB]為達到特定 BER(如 10⁻⁷)所需的最小載雜比。數值越高,表示對通道品質要求越高。
所以當環境極好時,就可以調到32APSK的最後一個選項,實現高速傳輸